Course, People
Work on Reflection A for
Wednesday
READING & HOMEWORK ASSIGNMENTS
Assignments are listed here chronologically by due date. New assignments will tend to be at the bottom of the page.
Last modified:
Jump directly to Week 1 | Week 2 | Week 3 | Week 4 | Week 5 | Week 6 | Week 7 | Week 8 | Week 9 | Week 10
The author of the textbook maintains a list of errata.
| DAY | BEFORE CLASS | IN-CLASS TOPIC/ACTIVITY |
|---|---|---|
| Mon 1 | ||
| Wed 1 |
To Be Submitted on
Kit
Readings
Chapter 0 (Everything after Section
0.1 should be review)
Section 1.1
|
Discussion Questions
Give state diagrams of deterministic finite automata recognizing the
following languages. In all cases the alphabet is {0,1}.
New material for small groups
Start working on
Problems 1.14 and 1.48 from Sipser
|
| Fri 1 |
To Be Submitted on
Kit
Problem
Readings
Read Section 1.2
Read Section 1.3
|
Discussion Questions
Finish new material from W1 (equivalence of NFAs and
DFAs)
Give NFAs with the specified number of states recognizing
each
of the following languages.
In all cases the alphabet is {0,1}.
Exercise 1.16 a.
Exercise 1.16 b.
The class of regular
languages is closed under union.
The class of regular
languages is closed under concatenation.
The class of regular languages
is closed under intersection.
The class of regular
languages is closed under the star operation.
Exercise 1.15.
New material for small groups
Give regular expressions generating the following languages.
In all cases the alphabet is {0,1}.
(The following are parts b, d, f, j, a nd l of Exercise 1.18.)
Lemma 1.55.
Example 1.58.
Describe the idea behind the proof of Lemma 1.60,
define GNFAs.
Example 1.66.
Example 1.68.
Exercise 1.21 b.
Work on
Problems 1.31 and 1.32 from Sipser
|
| Mon 2 |
To Be Submitted
on Kit
Problems 1.14 and 1.48
Readings
Be sure you've read all of Sections 1.2 and 1.3.
|
Discussion Questions
(Jenny, Tristan) Are the regular expressions 0*(10+)*1* and (0 U 10)*1*
equivalent?
(Aiden, Addie - part a, Logan, Ryan - part
b) Exercise 1.19, parts a and b.
(Dillon, Kevin) Part c of Exercise 1.28.
(Narelle, Maddie) (The following is Problem 1.36.)
Let Bn = { ak | where
k
is a multiple of n}.
Show that for each n >= 1, the language Bn is
regular.
New material for small
groups
Finish new material from F1.
|
| Wed 2 |
To Be Submitted
on Kit
Problems 1.31 and 1.32
Readings
Begin to read Section 1.4.
|
Discussion
questions
Student discussion questions from Mon
2
In-class Exercises
Convert the NFAs from Figures 1.6 and
1.42 to regular expressions.
Work through Exercise 1.21
Work through Exercise 1.22
Find a RE for the language of strings over the
alphabet {a, b} that do not contain the substring
aba.
Homework
Convert the NFA in the diagram below to a
regular expresssion. Follow the process outlined in
Theorem 1.60 and show your work.
 |
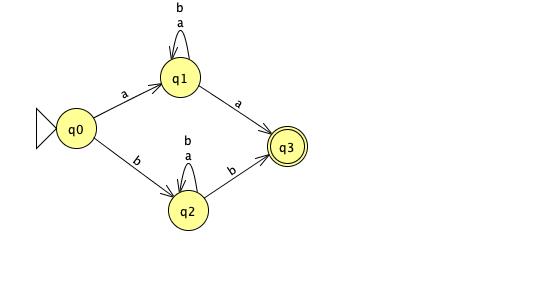| Fri 2 |
To Be
Submitted on Kit
NFA to RE conversion from Wednesday Week
2
Readings
Be sure you've read Section 1.4.
Watch the video What is the Pumping Lemma
Watch the video Nonregular languages: How to use the Pumping
Lemma
|
Discussion
Questions
TBD
New material
Theorem 1.70
Example 1.73
Exercise 1.29
(The following is Exercise 1.30.)
Describe the error in the following "proof" that
0*1* is not a regular language.
(An error must exist because 0*1*
is
regular.)
The proof is by contradiction.
Assume that 0*1* is regular.
Let p be the pumping length for
0*1* given by the pumping lemma.
Choose s to be the string
0p1p.
You know that s is a member of
0*1*, but Example 1.73
shows that s cannot be pumped.
Thus you have a contradiction.
So 0*1* is not regular. Exercise 1.55
Homework problems
Prove that the language {w | w is a palindrome}
over the alphabet {0, 1} is not regular.
(A palindrome is a string that reads the same forward and
backward.)
Problem 1.35 (Come see me if you need a hint for what
string to choose).
|
|
Mon 3
|
Readings
Make sure you've read Section 1.4
|
Discussion
Questions:
Finish material from Fri 2
Want a little more of a challenge? Try
Exercise 1.46
Work on HW problems from Fri 2
|
|
Wed 3
Fri 3 |
To Be
Submitted on Kit
Two problems from Fri 2 - 1) Language of palindromes
not regular and 2) Problem 1.35
Readings Read Section 2.1
|
New Material/Discussion Questions
Define context-free grammars
(CFGs) and give an example. Discuss process of designing CFGs. (ALL) Exercise 2.3. (part b - Sam, Pedro, part c - Joe,
Jessie, part e - Juniper, Judah) Exercise 2.4 (part b - Clara, Teddy) Exercise 2.6 (Zoie, Mollie) Discuss ambiguity and do exercise
2.8 (ALL) Consider the grammar with rules
(ALL) Exercise 2.16
Optional Challenge (For fun, not
credit) Discussion Problem:
Homework
Exercise 2.13
Reflection
Regular Language
Reflection (Due W4)
|
| Mon 4 |
To be Submitted on
Kit
Exercise 2.13
Readings
Read Section 2.2
|
Discussion Questions
and New
Material
Theorem 2.9
Example 2.10
Problem 2.26
Definition 2.13
Examples 2.14, 2.16, 2.18
Exercises 2.5 b, c, e
Exercise 2.7
Theorem 2.20
Exercise 2.11
Problem 2.18
Homework Problems Exercises 2.14, 2.17
|
| Wed 4 |
To be Submitted on
Kit
Regular Language Reflection
Readings Finish reading
Section 2.2
|
Continue with Monday's material, starting
from Exercise 2.5
Keep working on homework exercises
2.14, 2.17 (due F4)
|
| Fri 4 |
To be Submitted on
Kit:
Exercises 2.14, 2.17
Reading Reread any parts of Section 2.2
that you need. If you are caught up you may
start reading Section 2.3.
Watch this video example of converting a PDA to a
CFG
|
Discussion Questions and
New Material:
Convert the following grammar into Chomsky Normal Form:
S -> ( S ) S Describe the language generated by this
grammar.
Work through equivalence of languages accepted by
PDAs and languages generated by context free grammars.
Work on
homework as time permits
Homework Problem Exercise 2.12
|
| Mon 5 |
To Be Submitted on
Kit
Exercise 2.12
Readings Read Section 2.3
|
Discussion Questions and
New Material:
Theorem 2.34
Examples 2.36, 2.37, 2.38
Work on Problem 2.30
|
| Wed 5 |
Readings
Read Section 3.1
|
Discussion Questions and
New Material:
Discuss Problem 2.30
Discuss Problem 2.18 (done on M5)
Introduce definitions (Turing machine, various types of
configurations, Turing-recognizable, Turing-decidable)
Homework Problem Exercise 2.2
|
| Fri 5 |
To be
Submitted on Kit:
Exercise 2.2
Readings Read Section 3.1.
Explore the TM examples listed under the
Discussion Questions
|
Discussion Questions and New Material
Definitions (Turing machine,
various types of configurations, Turing-recognizable,
Turing-decidable)
Example 3.7.
Example
3.9.
Example
3.11.
Example
3.12
Exercise 3.2
(d).
Exercise 3.5.
Exercise 3.7.
Exercise 3.8, giving higher-level
descriptions. (To be done in groups and submitted)
Look at
examples
#1-6 of Turing Machines. Describe the languages recognized by these
machines. (Some of you explored these a little in COMP105, but some
of you never took COMP105. In either case, it's good to take a look
at them now with more experienced eyes!)
Problem 3.15.
Problem 3.16
Homework Context-free
language reflection (due Wed 6)
|
| Mon 6 |
To
be Submitted on Kit:
Exercise 3.8 from class on F5
Readings
Read Section 3.2
|
Discussion Questions and New
Material
TBD
|
| Wed 6 |
To be
Submitted on Kit:
Context-free language reflection
Readings Read Section 3.3.
Read the Chapter on Turing "Turing Conceives of the All-Purpose
Computer" that is posted on Kit.
Check out these videos to see physical Turing machines that people have actually built:
|
Discussion Questions and New
Material
Finish DQ and new material from Mon 6
Theorem 3.13
Theorem 3.16
Corollaries 3.15, 3.18, 3.19
Explain the difference between a decider and a
recognizer.
Homework Problem Problem 3.11
|
| Mon 7 |
Readings
Be sure to have read Sections 3.2 and
3.3
|
Discussion Questions and New
Material
Finish DQ and new material from F6
Church-Turing Thesis
Algorithms and Turing machines
Homework Problem
Research real-world applications of DFAs, NFAs, PDAs, CFGs. Find two that are interesting to you and
submit a short summary of each. At the end of your summaries, you should include any links or references to the applications you found.
|
| Wed 7 |
To be
Submitted on Kit
Problem 3.11
Reading Read Section
4.1.
|
Discussion Questions and New
Material
Theorem 4.1.
Theorem 4.2.
Theorem 4.3.
Theorem 4.4.
Theorem 4.5.
Theorems 4.7 - 4.9.
Exercise 4.2.
Exercise 4.3.
Exercise 4.5.
Exercise 4.6.
Problem 4.10.
Problem 4.16.
Problem 4.25.
|
| Fri 7 |
DOGL
|
|
| Mon 8 |
Readings
Finish Section 4.1
Start Section 4.2
|
Discussion Questions and
New Material
Theorems 4.7 - 4.9 (from Week 7)
Problems 4.11, 4.12
Work on getting previous homework
finished
Homework
Problems
Problems 4.13, 4.21, 4.26, 4.28
|
| Wed 8 |
Readings
Keep reading Section 4.2
|
Work on homework problems
|
| Fri 8 |
Readings
Finish reading Section 4.2
|
Discussion Questions
and New Material
Theorem 4.11
Corollary 4.18
Theorem 4.22
Corollary 4.23
|
| Mon, Wed 9 |
Readings
Read Sections 5.1 and 5.3
|
Discussion Questions
and New Material
Theorem 5.1 - 5.4
Theorem 5.13
Exercises 5.1, 5.2
Problem 5.13
Theorem 5.22, Corollary
5.23
Examples 5.24, 5.26
Theorem 5.28, Corollary
5.29
Theorem 5.30
Exercise 5.5
Problem 5.28 (Rice's
Theorem)
Homework Problems Problems 5.9, 5.22 (You may submit
these in groups, one person submits and invites the
others on Kit)
|
| Fri 9 |
Readings
Read Sections 7.1, 7.2
|
Discussion Questions
and New Material
Definitions 7.2, 7.5 and their
examples
Definition 7.7 and the example
involving the language A =
{0k1k | k
>= 0}.
Theorem 7.8
Definition 7.9
Theorem 7.11
Definition 7.12
Theorems 7.14, 7.15, 7.16
Exercises 7.1, 7.2, 7.8,
7.9
Reflection Work on the Relfection on Context Free, Turing-Decidable, and
Turing-Recognizable Languages before Friday of Week 10
|
| Week 10 |
Reading
Read some more in Chapter 7
|
Discussion Questions
and New Material
Group discussion of P, NP,
NP-Complete. Submit summary on Kit
Complete your Final
Reflection by NOON on
Tuesday, June 6.
|
Week 7: Thursday
- Small group meetings to go over decidable problems from DQs
Week 7: Friday
- Homework problem for Friday of Seventh Week:
- Problem 3.11. (If you haven't already submitted it on W7.)
- Reading Assignment for Friday of Seventh Week:
- Section 4.2.
- Discussion Questions and New Material for Friday of Seventh Week:
- No class meeting
- Reading Assignment for Monday of Eighth Week:
- Finish reading Chapter 4.
- Discussion Questions and New Material for Monday of Eighth Week:
- Exercise 4.5 (not in 2nd edition).
- Problem 4.10 (4.9 in 2nd edition).
- Problem 4.16 (4.15 in 2nd edition.
- Problem 4.25 (4.23 in 2nd edition).
- Theorem 4.11.
- Corollary 4.18.
- Theorem 4.22.
- Corollary 4.23.
- Homework problems for Friday of Eighth Week:
- Problems 4.13 (4.12 in 2nd edition), 4.21 (4.19 in 2nd edition), 4.26 (4.24 in 2nd edition), 4.28 (4.26 in 2nd edition).
- Reading Assignment for Wednesday of Eighth Week:
- Read Sections 5.1, 5.3.
- Discussion Questions and New Material for Wednesday and Friday of Eighth Week:
- Theorem 4.11.
- Corollary 4.18.
- Theorem 4.22.
- Corollary 4.23.
- Theorem 5.1.
- heorem 5.2.
- Theorem 5.3.
- Theorem 5.4.
- Exercise 5.1.
- Exercise 5.2.
- Problem 5.13.
- Theorem 5.22 & Corollary 5.23.
- Example 5.24.
- Example 5.26.
- Exercise 5.5.
- Problem 5.28.
- Exam 2 will be available by the end of Eighth Week, and will be due by the end of Ninth Week.
- Small groups to go over decidabilty Thms and DQs
Week 9
- Reading Assignment for Ninth Week:
- Read Sections 5.1, 5.3.
- Discussion Questions and New Material for Ninth Week:
- Start/Continue with Reducibilty Thms and Exercises
- Theorem 5.1.
- Theorem 5.2.
- Theorem 5.3.
- Theorem 5.4.
- Exercise 5.1.
- Exercise 5.2.
- Problem 5.13.
- Theorem 5.22 & Corollary 5.23.
- Example 5.24.
- Example 5.26.
- Theorem 5.28, Corollary 5.29.
- Theorem 5.30.
- Exercise 5.5.
- Problem 5.28.
- Homework Questions for Tenth Week:
- Problems 5.9 and 5.22. These may be done in groups, where each group submits one set of solutions with all group member names.
- Reading Assignment for Tenth Week:
- Read Chapter 7.
- Discussion Questions and New Material for Tenth Week:
- Definitions 7.2, 7.5 and examples.
- Definition 7.7 and example involving language A = {0k1k| k >= 0}.
- Theorem 7.8.
- Definition 7.9 & Theorem 7.11.
- Exercise 7.5.
- Exercise 7.6.
- Exercise 7.7.
- Exercise 7.12.
- Definition 7.12.
- Theorem 7.14.
- Theorem 7.15.
- Theorem 7.16.
- Problem 7.15.
- Exercise 7.8.
- Exercise 7.10.
- The final reflection will be distributed on or before Wednesday, and will be due on Kit by Monday, June 7.