Lab: Traversing 2D Data Structures
Using Iterators
Introduction
In this lab you will implement the iterators for several algorithms that step
through (traverse) a two-dimensional data structure made up of rows and columns.
These algorithms are useful for many different kinds of two-dimensional data
structures.†
The two-dimensional data structure used in this lab is represented by a BoundedGrid object
made up of rows and columns.‡ A BoundedGrid object
models a bounded rectangular grid that contains objects at various grid locations.
Each cell contains zero or one objects. In this program, cells that are
not empty will contain color blocks (objects of the ColorBlock class).
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
|
| 1 |
| 2 |
| 3 |
We refer to locations in the grid by their row and column numbers in parentheses,
such as location (2, 7). Row and column numbers start at 0 rather than 1, so
location (0, 0) refers to the first row and first column. Object obj1 in
the grid shown above is in the first row and fourth column, or at location
(0, 3). Object obj5 is at location (3, 8). (This is similar to
the way Java array and ArrayList indices are numbered.)
A traversal through a two-dimensional data structure is an algorithm
that steps through all the elements of the data structure, visiting each element
exactly once. A traversal through a grid steps through all the
locations in the grid. There are many different ways to traverse
through a grid. One common type of traversal is a row-major
traversal, which steps through the grid row-by-row. It first
visits all the locations in row 0, then all the locations in row 1, and
so on.
Another common traversal is a column-major traversal, which steps through
the grid column-by-column. It first visits all the locations
in column 0, then all the locations in column 1, and so on.
In this lab you will define iterator classes that implement various traversal
algorithms. For example, the following simple code uses the RowMajorGridIterator
iterator, which steps through a grid in row-major order.
RowMajorGridIterator it = new RowMajorGridIterator(env);
while ( it.hasNext() )
{
Location nextLoc = (Location) it.next();
new ColorBlock(highlightColor, env, nextLoc);
}
The iterator classes you define will be used in a program that defines buttons
for the various traversal algorithms and then illustrates each algorithm by
placing color block objects in the grid in the order of the traversal.
Not all of them will be true traversals, in which every location is visited
exactly once, but all will step through grid locations in some specific
pattern.
Getting Started
In this lab you will be implementing new iterator classes and adding them
to the list of iterators used by the IteratorLab application. The
first thing to do, therefore, is to download the existing code for this application.
Exercise Set 1
- Download the zip file that contains the starting code files for
the Grid Iterator Lab (
GridIterator.zip)
and unzip it. You will see the following files and folders.
- The
Instructions folder
contains this write-up (GridIterator.shtml).
- The
grid.jar Java archive (jar) file
contains a library of classes that can be used to model a two-dimensional
grid as described above.
BoundedGrid (class that represents the two-dimensional
grid)‡Location (class that represents the row and column
positions of a location in the grid)‡ColorBlock (class whose objects represent blocks
of color put in a grid)
- The
GridPkgClassDocumentation folder contains the class
documentation for
the classes in the grid.jar library.
- The
JavaSourceFiles folder contains the source
files for the Grid Plotter program in which we can draw pictures
by placing (plotting) color blocks in a grid.
IteratorLab (contains the main method)GridIterator class (the abstract iterator class
you will be extending)
RowMajorGridIterator (an iterator class that
implements a row-major traversal; you can use this as a template
for other iterator classes)ColMajorGridIterator (a skeleton iterator class
that you fill in)
IteratorGUI (a class that implements the program's
graphical user interface; you are not expected to read or understand
this class)IterationController (a class used by the program's
graphical user interface to control the traversals; you are not
expected to read or understand this class)
- You can find documentation for
these files in the
GridIteratorClassDocumentation folder.
Note: All of the
classes in the JavaSourceFiles folder and the grid.jar Java
archive file are
covered by the GNU
General Public License.
- Compile and run the program. As the program starts up you will be
asked for the dimensions (number of rows and columns) of the grid
in which you will be drawing. For now you can go with the default
values, since your purpose for this exercise is just to experiment
with the user interface. Once you have chosen the grid dimensions,
click on the "Row-Major Order" button, you should see color
blocks filling the locations of the grid in row-major (top-down,
left-to-right) order. Experiment with the speed adjustment slider
while the program is drawing color blocks.
- Experiment with the program to discover what the "Create New
Grid" and "Clear" buttons and the "Background
Color" and "Drawing Color" menus do. What happens
if you press the "Row-Major Order" button twice in a row?
- Experiment with the "Column-Major Order" button.
What is printed to
System.out? What happens if
you click on the "Stop" button after a couple of iterations?
What happens if you let the traversal run indefinitely?
|
Studying the Algorithms
The starting point of the Grid Iterator application is the
IteratorLab class, which contains the main method. Look over the class.
It defines two constants that define the size of the window containing
the graphical user interface and two more that define the extreme values for
the speed adjustment slider. The class's main method establishes
what traversal algorithms are supported and then creates the graphical user
interface and makes it visible on the screen. The IterationController.register
method is a class method that associates an algorithm name (which becomes the
label on a button) with the iterator class that implements that algorithm.
Exercise Set 2
- Experiment with the constants defined at the top of the
IteratorLab class to see how changing them affects the application.
|
Next, look at the ColorBlock class, which pairs a color and location
together. The Color class is a standard Java class found in java.awt.
You can create a color by specifying amounts of red, green, and blue (values
between 0 and 255), or you can use one of the predefined colors provided in
the class, such as Color.red. The Location class comes
from the AP® Marine Biology Case Study.‡
java.awt.Color Class (Selected Constants
and Methods)
BLACK, BLUE, CYAN, GRAY, GREEN,
MAGENTA, ORANGE, PINK, RED, WHITE, YELLOW
Color(int r, int g, int b) |
Exercise Set 3
- What aspects of the
ColorBlock class allow its objects
to be put in a grid? How do ColorBlock
objects get added to a grid? Is the ColorBlock
class needed? Couldn't we just put Color objects
in a grid?
|
Finally, we get to the heart of the IteratorLab application, the
set of traversal algorithms it supports. These are implemented using iterators
that step through a grid, as in the code example in the Introduction
section of this lab. The GridIterator abstract class partially
implements the standard Java Iterator interface; the RowMajorGridIterator
class is one example of a concrete subclass of GridIterator that
completes the implementation. In particular, the Iterator
interface specifies that all iterator classes need to define hasNext
and next methods (used in the code example in the Introduction).
The abstract GridIterator class implements these methods, but the
implementation of the next method makes use of a protected, unimplemented
findNextLocation method. This method must be implemented
in concrete subclasses of GridIterator, such as RowMajorGridIterator.
The way findNextLocation is implemented in each concrete subclass
determines how the iterator traverses the grid. Each concrete subclass
of GridIterator must also provide a constructor that takes a BoundedGrid
as a parameter, since that is what the TraversalGUI object assumes
is available when it tries to construct a concrete iterator object.
Exercise Set 4
- Does the code example in the Introduction section
behave correctly if the grid is empty?
- Can you create an
Iterator instance? A GridIterator
instance? A RowMajorGridIterator instance?
- Looking at the
GridIterator class, what is the first
location returned by the next method? Does this
depend on the specific implementation of findNextLocation
used by an iterator object?
- How do the statements in the
findNextLocation method
of the RowMajorGridIterator class ensure that the order
in which the application highlights cells will be row-major order?
|
Adding New Algorithms
Now it's time to write some iterators for traversal algorithms of your own.
Exercise Set 5
- Complete the
ColMajorGridIterator class, using RowMajorGridIterator
as a guide. Test your class by running the program and watching the
traversal. Are the cells highlighted left-to-right, going down each
column?
- Create a
ReverseRowMajorGridIterator class, using RowMajorGridIterator
as a guide. This algorithm should highlight cells bottom-up, going
left-to-right across each row. In other words, the row order is
reversed,
but the column order is not. Edit the main method in the IteratorLab
class to register your new class with an appropriate name. Test
your new class by running the program and watching the traversal.
Remember that each concrete subclass of GridIterator
must provide a constructor that takes a BoundedGrid as
a parameter. That constructor could use either of the constructors
in GridIterator: the one that takes only a bounded grid as a
parameter, or the one that takes both a bounded grid and a
starting location.
- Create a
ReverseColMajorGridIterator class, using ColMajorGridIterator
as a guide. This algorithm should highlight cells right-to-left, going
up each column from the bottom. In other words, both the row and column
orders should be the reverse of ColMajorGridIterator.
Test your new class.
- Create a
Diagonal class. This algorithm should highlight
cells along the diagonal from the upper-left corner to the lower-right
corner.** Again, it is not a true traversal of the grid.
Before you attempt to write the code, list the locations that you
want the iterator to visit. When you're done with the implementation,
test your new class.
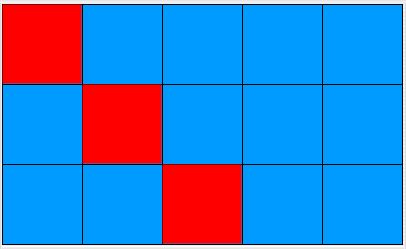
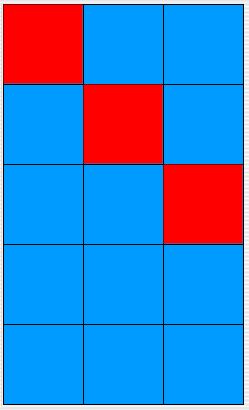
**The diagonal algorithm goes to exactly the lower-right corner only
if the grid is square. If it is not square, the algorithm
traverses down and to the right until it comes to the last column
or the last row, depending on whether the grid is higher than
it is wide or wider than it is high. The diagrams below show the behavior
for a 5 x 5 grid, a 3 x 5 grid, a 5 x 3 grid,
and a 1 x 1 grid.
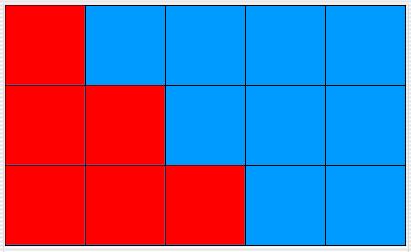
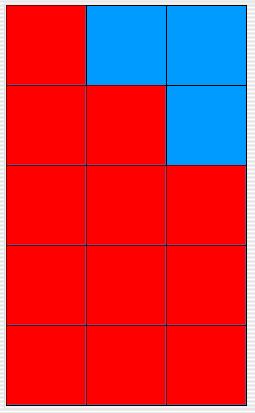
- Create a
Triangle class. This algorithm should highlight
(fill in) all the cells below the diagonal you produced in the preceding
exercise. (It will form a true triangle only if there are at least
as many columns in the grid as there are rows.) Before
you attempt to write the code, list the locations that you want the
iterator to visit. When you're done with the implementation, test
your new class. The diagrams below show the behavior for a 5 x 5 grid,
a 3 x 5 grid, a 5 x 3 grid, and a 1 x 1 grid.
- Create a
DoubleDiagonal class. This algorithm should
highlight the cells along the two diagonals, from the upper-left corner
to the lower-right corner** and from the upper-right corner to the
lower-left corner.** If the grid has an odd number of columns,
the two diagonals will cross at a single location, but your "iterator"
should not return that location twice. Before you attempt to
write the code, list the locations that you want the iterator to visit.
When you're done with the implementation, test your new class. (**Again,
whether the algorithm goes exactly to the opposite corner depends
on whether the grid is square.) The diagrams below show
the behavior for a 5 x 5 grid, a 4 x 5 grid, a 5 x 4
grid, and a 1 x 1 grid.
Hints: You can draw the double diagonal by drawing a line from
the upper-left corner down and to the right and drawing a line from
the upper-right corner down and to the left. OR, you
can visit both locations in the first row, followed by both locations
in the 2nd row, etc. This algorithm may be easier.
You know one of the two locations in each row from your implementation
of the Diagonal class, and you can calculate the other
from it, given the number of columns in each row. You'll
need a way of recognizing whether you're visiting the first location
in a row, in which case the next location should be the other location
in the row, or visiting the second location, in which case the next
location will be on the next row. If both locations are the
same location (single cross-over point), then you do not want to visit
it twice.
- Create a
PerimeterTraversal class. This algorithm should
highlight the cells along the four sides of the grid, but not
the interior cells. This is actually a traversal of the grid's
perimeter rather than of the grid as a whole, because you will
not be visiting every location in the grid. Before you
attempt to write the code, list the locations that you want the iterator
to visit in order to find a pattern. When you're done with the implementation,
test your new class. The diagrams below show the behavior for
a 5 x 5 grid, a 2 x 5 grid, a 3 x 1 grid, and
a 1 x 1 grid.
- Create a
SpiralTraversal class. This algorithm should
highlight the cells along the perimeter of the grid, then spiral
in and highlight the cells along the perimeter of the unhighlighted
cells, then spiral in again and highlight the next perimeter of unhighlighted
cells. Continue in this way until you have visited every location
in the grid. Before you attempt to write the code, list
the locations that you want the iterator to visit in order to find
a pattern. When you're done with the implementation, test your new
class.
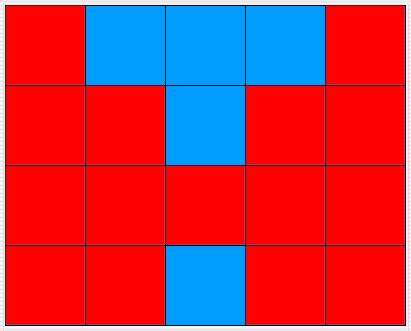
- Create a
Butterfly class. This algorithm should highlight
the cells in the left and right side quadrants formed by the double
diagonal you produced in Exercise 6. Before you attempt to write the
code, list the locations that you want the iterator to visit. When
you're done with the implementation, test your new class. (See previous
exercises to read more about square and non-square grids.)
The diagrams below show the behavior for a 5 x 5 grid, a 4
x 5 grid, a 5 x 4 grid, and a 1 x 1 grid.
|