involves running 100 experiments for 21 different conditions. That's 2,100 clicks of the run button. If we want to run 1,000 experiments for each condition we end up with 21,000 clicks.
Our graphical percolation program is great for visualizing the percolation process. However in its current form it is not ideal for running experiments. Imagine we want to answer the following question:
"What is the probability that a gas will percolate from the top row to the bottom row in a 100x100 grid, given that each cell has a 30% chance of being blocked?"
Your first instinct might be to start the program, create an appropriate grid, and click run. What would you be able to conclude from the result? Not much. The fact that the material reached the bottom (or didn't) tells us very little about what will happen the next time we run the experiment. In order to obtain a meaningful answer, we need to run the experiment many times and average the results. If we run this experiment 1,000 times, and the material percolates 234 times, we can be confident that the probability of percolation for these conditions is somewhere around 23%.
Clicking
the run button 1,000 times is not an attractive option.
Running these experiments by hand will be even less attractive if we
want to systematically explore the effects of changing the probability
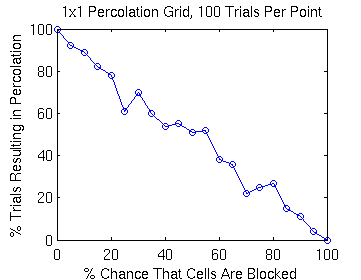
that cells are blocked. Generating a figure like this:

involves running 100 experiments for 21 different conditions. That's
2,100 clicks of the run button. If we want to run 1,000 experiments for
each condition we end up with 21,000 clicks.
The purpose of this project is to modify the Percolation program to automate the process of obtaining results like those described above, and then to use the updated program to obtain some experimental results.
Up until now, we have placed the initial percolators by hand using the "Manually Populate Grid" button. For the purposes of experimentation we want this process to be automated. At the beginning of each experiment the entire grid should be randomly populated with solid cells, and each empty cell in the top row should be populated with the appropriate type of percolator. There is code in place to handle this.
The first step is to uncomment several lines
in PercolationApp. Somewhere around line 87 you should
see the following statement:
Class[] percTypes = {
// VerticalPercolator.class,
// GravitationalPercolator.class,
// AllDirectionPercolator.class
};
Remove the comments and, if necessary, update the names to match the
names you used for your percolator classes. The percTypes
array will be used by the program to generate a pull-down menu of
percolator types. Compile and run your updated program. Experiment
with selecting a percolator type and clicking on the "Automatically
Populate Grid" button. You should find that the top row is
automatically populated with the appropriate percolator type. You
will also observe that two additional buttons have been added to the
GUI: "Run N Times" and "Run Density Experiments". Try clicking these
buttons. You will be prompted for the appropriate experimental
parameters, but the experiments will not run. The next step in the
project is to write the code that executes the requested
experiments and prints the results.
The "Run N Times" and "Run Density Experiments" buttons each result in
a call to corresponding methods in
the PercolationController class, runNTimes
and runExperiments.
The basic logic for the runNTimes method should be as follows:
repeat N times:
Randomly fill in the grid using the appropriate density.
Fill in the top row of the grid with percolators.
Run the percolation simulation (without involving the GUI).
If any material percolated to the bottom, increment a counter.
After all N runs have completed, use System.out.println to print a summary
of the results including:
The size of the grid.
The density.
The number of runs.
The number of runs that resulted in percolation.
There are several existing methods in
the PercolationController class that will be useful for
implementing runNTimes. These
include randomlyFillGrid, fillTopRow, invisibleRun
and percolatedToBottom. Read each of these methods, along
with their comments, to make sure that you understand what they do and
how to use them.
Notice that we want to avoid updating the GUI while these experiments are running. While it might be entertaining to watch thousands of percolation experiments, (it might make a good screensaver) the experiments can be run much more quickly if the GUI is not involved. This is one of the motivations for maintaining a separation between the code that handles the GUI and the code that handles the simulation logic.
Implement and test the runNTimes method.
Once you have completed the runNTimes method,
implementing runExperiments should be straightforward. It
will consist of a loop that repeatedly calls runNTimes with an
appropriate series of density values. Implement and test the
runExperiments method. (Note that there are two stub methods
in the PercolationController class named
runExperiments. You will be modifying the version that takes
three arguments. Disregard the version that takes zero arguments.)
In your programing studies so far, perhaps you haven't worried very much about writing efficient code. Computers can execute many millions of instructions per second, so a slightly more efficient implementation of a small, relatively simple program is unlikely to make a noticeable difference to the user. The situation here is different. The code you wrote above allows you to easily run tens of thousands of percolation experiments with just a few mouse clicks. Even if each of those experiments only takes a fraction of a second, the entire process could take minutes or hours. For example, assume that for a given grid size it takes .1 seconds to complete a single percolation experiment. If we want to complete 1,000 runs at 20 different densities, the total time will be: 1,000 * 20 = 20,000 runs * .1 seconds/run = 2,000 seconds = 33 minutes.
The next step in the project is to run some experiments to get a feel
for the performance of the current version of the code. Fill in the
following table by using a stopwatch to time the program. (The specific
number of runs in this table are examples. Depending on the speed of your
computer, you may need to increase the number of runs significantly —
maybe even by a factor of 10 or more — to see significant differences
in the times.) Each entry in the table should contain the time, in seconds,
that it took the program to complete under the given conditions. Use the
AllDirectionPercolator for these experiments. Save these
results to be submitted along with your finished programming project.
| 25x25 grid | 50x50 grid | 100x100 grid | |
|---|---|---|---|
| 50 runs | |||
| 100 runs | |||
| 200 runs |
Is it possible to do better than this? Take a few minutes to read
over the step method of the
SlowPercolationController. This method works by iterating
through the entire grid, placing every object it finds into an ArrayList,
and calling act on each of those objects. This is inefficient
in at least two different ways. First it is possible that the grid is
mostly empty. In that case the code may loop through many hundreds of grid
positions just to find a small number of objects. Second, it is likely that
most of the objects being asked to act will not do anything. The act
method will have no effect on solid material or on percolating material
that has no place to go.
Take another look at the results of your timing experiments and write answers to the following questions:
A more efficient approach is to explicitly keep track of the set of
items that needs to be processed. Any individual item in the
grid needs to have its act method called at most once.
Once an object has percolated to the appropriate neighbors, its work is
done and it no longer needs to be considered.
The source code provided to you includes the skeleton of
a ListPercolationController class that will take
advantage of this. The basic idea is to maintain two lists of grid
objects. One list (processThisStep) will represent the
set of items that needs to be processed in the current step, and the
other (processNextStep) will contain the list of objects
that needs to be processed in the next step. Every time a new object
is added to the grid as a result of percolation, it is also added to
the list of items that will be processed on the next step.
The process completes whenever there is a step that adds no items to the
processNextStep list.
Complete and test the ListPercolationController by
following the comments in the method stubs. You can test the
controller by selecting it in the pull-down menu of the GUI. Once you
are sure that your code is working correctly, re-run the timing
experiments above using the new controller. Record the results to be
submitted with the completed project. Type answers to the following questions
for your new set of results:
For large grids, percolation systems like the one we are looking at experience a threshold effect: if we gradually increase the percentage of blocked grid squares, at some point the probability that the material will percolate drops from 100% to 0% almost immediately. The goal of this exercise is to estimate where that drop-off occurs. Pick either the gravity percolator or the all directions percolator and estimate the value of the threshold. The threshold will be the place where there is a 50/50 chance that the material will percolate. For these experiments you should use grids of size at least 100x100, with at least 1,000 runs per density. You will get better results with larger grids.
You can start out by running experiments across a wide range of densities, say from 0%-100% in 10% intervals. Those results should allow you to narrow your experiments down to a smaller region where you can run experiments using smaller intervals. Since we have implemented our probabilities as integer values, you won't be able to narrow down your estimate much beyond the closest percentage point. That's OK. Type up a paragraph describing your results and presenting your estimate. You should also include a copy of the raw data that you used to reach your conclusion. You will submit these results along with your completed project.
If you are interested, there are many other experiments you could run using this system: how exactly does the size of the grid change the sharpness of the threshold? Does the shape of the grid matter? In other words, would the probability of percolation be the same for a 100x100 grid as for a 20x500 grid (both have 10,000 entries)?
Submit your answers to the questions above, along with the Java source
files for your four completed percolator classes, the completed
PercolationController class and the
ListPercolationController class.