Boolean Expressions, Truth Tables, and Circuit Diagrams

Write your answers to the questions below in the provided Markdown template and submit it to Kit.

Boolean Expressions, Truth Tables, and Circuit Diagrams

For any given Boolean expression, we can develop a circuit diagram (sometimes several different circuit diagrams) implementing the same logic. In other words, for any given set of inputs, the Boolean expression and circuit diagram will produce the same True/False output. We can also express the logic represented by a Boolean expression or circuit diagram with a truth table. We can go the other direction also: we can represent any given truth table as an equivalent Boolean expression or circuit diagram.

For example, the logical Boolean expression Z = A AND NOT B (or Z = A * B') and the circuit diagram and truth table below all represent the same logic.

A     B   Z

A   B   B'  A * B' 0 0 1 0 0 1 0 0 1 0 1 1 1 1 0 0

Exercises

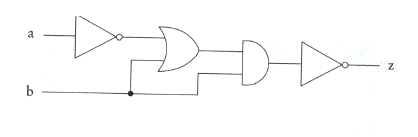
1. The next two questions refer to the following circuit diagram:

   a
   		z
   b

   • Provide the Boolean expression (in terms of a and b) for the output z in this circuit diagram.
   • Provide a truth table that shows the inputs a and b and the output z corresponding to this circuit diagram.

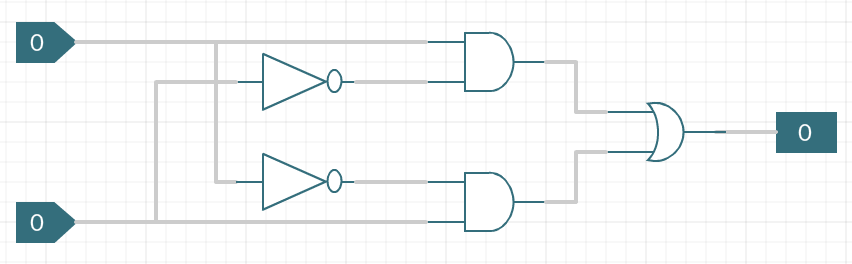
2. The next two questions refer to the following circuit diagram:

   a           b   z

   • Provide the Boolean expression (in terms of a and b) for the output z in this circuit diagram.
   • Provide a truth table that shows the inputs a and b and the output z corresponding to this circuit diagram.
3. What similarities and differences do you notice between the two circuit diagrams, the two Boolean expressions, and the two truth tables? What do the similarities in the truth tables tell you about the Boolean expressions and circuit diagrams?

4. An "exactly one" function can be generalized to any number of inputs. No matter how many inputs there are, the output is true if and only if exactly one of the inputs is true. Construct a truth table for a 3-input "exactly one" function and write a Boolean expression that corresponds to that truth table. (In a future exercise, you will use a software package for creating circuit diagrams to draw a diagram that implements this truth table and Boolean expression.)

   Hint: Your Boolean expression will probably include AND clauses that include three terms. For example: A'B'C.

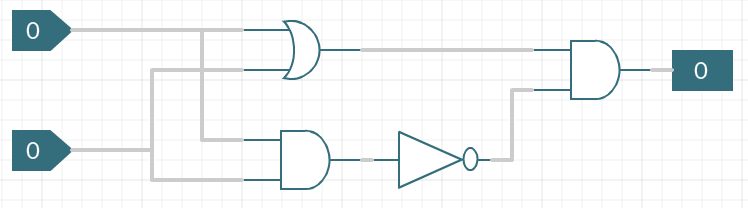
5. Consider the following (very inefficient) circuit diagram:

   
   • Provide the Boolean expression (in terms of a and b) for the output z in this circuit diagram.
   • Provide a truth table that shows the inputs a and b and the output z corresponding to this circuit diagram.
   • Based on the truth table you just created, could you create a simpler, logically equivalent Boolean expression and circuit diagram? If so, provide the Boolean expression. (You don't have to draw the corresponding circuit diagram.)