In-Class Activity:
Finite State Machines and Regular Expressions

Finite State Machines

This lab should be done individually, although you may certainly discuss your progress with your neighbors.

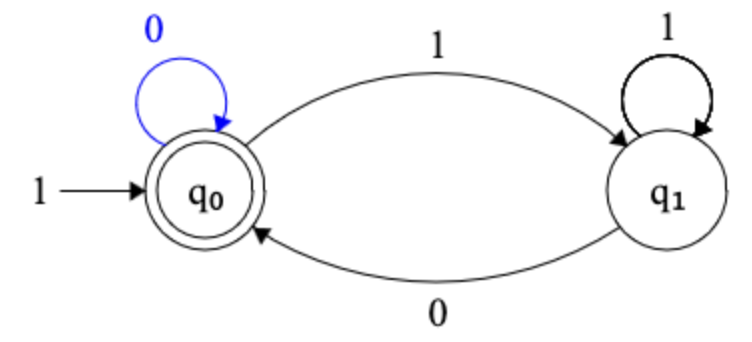
A Finite State Machine (FSM, also known as a Finite State Automaton, or FSA) is said to accept a given input string if the input takes the machine from the start state, indicated in these diagrams by a triangle, to an accepting (or final) state, indicated by a double border.

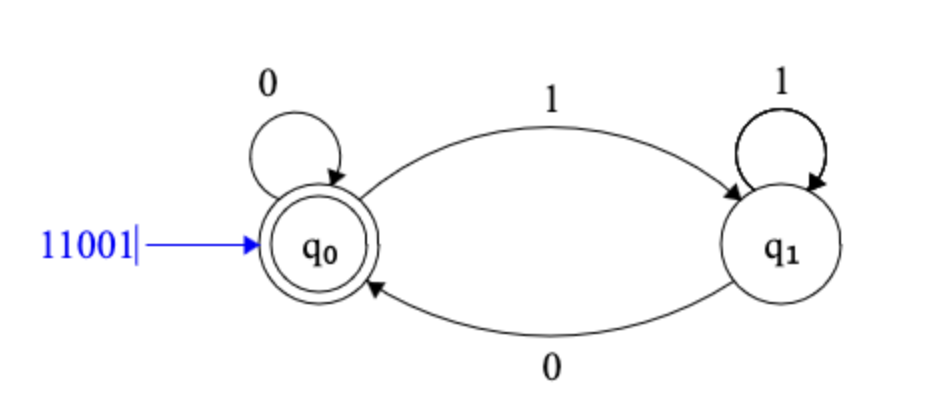
The diagrams below show how an example FSM behaves as it reads an input string (11001) from left to right. The first 1 causes the FSM to transition from q0 (the start state) to q1. The second 1 causes the FSM to stay in state q1. The first 0 causes the FSM to transition from q1 back to q0. With the second 0, the FSM stays in state q0; the last 1 moves the FSM back to q1. In this case, the input is not considered to be accepted by the FSM, because it ends up in state q1, not in q0, which is the accepting or final state for this machine.

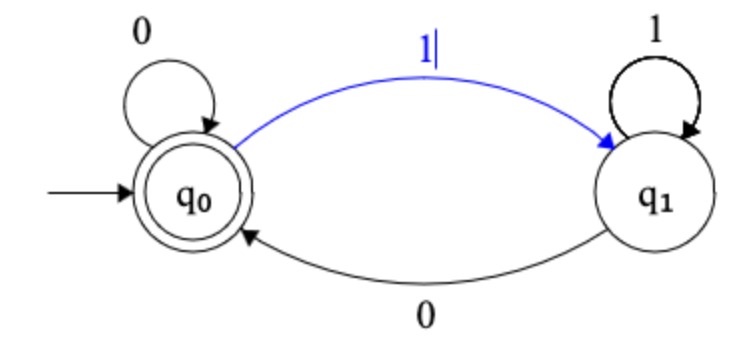
In these exercises, you will be reading and reasoning about Finite State Machines, and their closely-related cousin, Regular Expressions. In exercises 9, 10, and 13, you will draw Finite State Machines of your own. To do that you may use Evan Wallace's Finite State Machine Designer (used to draw the diagrams above). Alternatively, you may download JFLAP, a more complex graphical tool for experimenting with many concepts from automata theory (used to draw the diagrams below), but it also requires downloading the Java JDK or JRE. (You can find a copy of JFLAP in the CS 101 channel of the online Collaboration Center and a simple "cheat sheet" for using it here. A third alternative is to draw your three FSMs by hand.

Note for using Finite State Machine Designer:

Instructions for using the tool are on its web page, but if you have a Mac, you may need fn-Delete to delete objects. Also, you can use shift-click in a state to generate an arrow circling back to the state.

FSM Exercises

Write down answers to each of the numbered questions below.

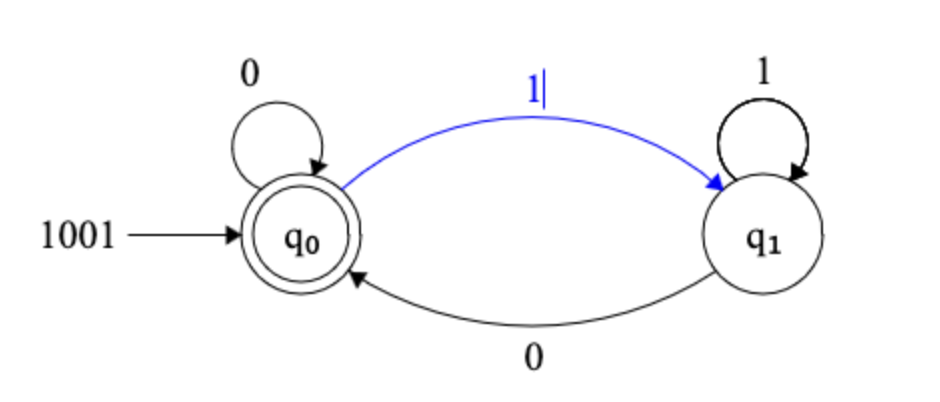
• Consider the following FSM:
  
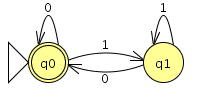
  1. Will this machine accept the string 1001? Will it accept 0010?
  2. Write down two additional strings that this FSM will accept.
  3. Write down two additional strings that this FSM will reject.
  4. Provide an English language description of the set of strings that this FSM accepts.

  (If you have installed JFLAP, you can try using it to check your answers above.)

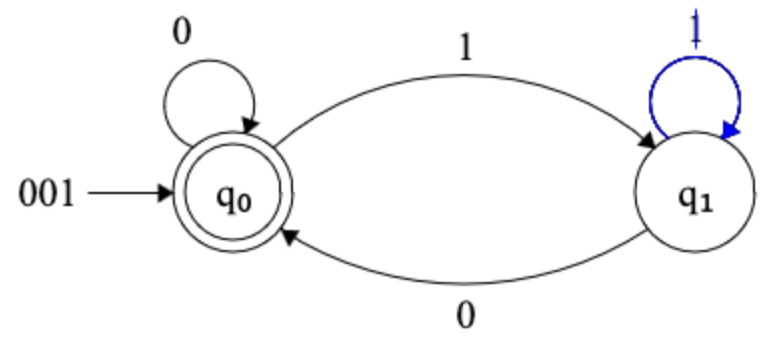
• Consider the following FSM:
  
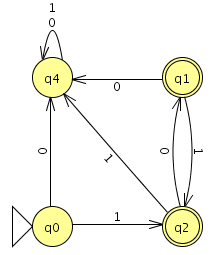
  5. Will this machine accept the string 1010? Will it accept 01010? 1010110?
  6. Write down two additional strings that this FSM will accept.
  7. Write down two additional strings that this FSM will reject.
  8. Provide an English language description of the set of strings that this FSM accepts.

  (If you have installed JFLAP, you can try using it to check your answers above.)

• Design FSMs that recognize the following two sets of strings. "Test" each of your designs by checking them with several strings that meet the criteria in different ways. Use the Finite State Machine Designer to draw your FSMs. (Or use JFLAP, or draw by hand.)
  9. The set of all strings of 0's and 1's that end in a 1.
  10. The set of all strings of 0's and 1's with an odd length.

Regular Expressions

Regular expressions provide another way of describing the sets of strings that are "accepted" by a finite state machine, i.e., for which the finite state machine will halt in an "accept" state. Binary strings are just sequences of 0's and 1's, such as, 0, 1, 01, 101, or 1100100011100111. An empty string has no items in it, i.e., has a length of 0. Regular expressions can be built using three different operators:

Concatenation (followed-by) - This is expressed by placing two symbols (or other regular expressions) adjacent to each other. For example, 01 represents the string of length 2 composed of a zero followed by a one; 1000001 represents the string of length 7 composed of a one, followed by five zeros, followed by a one.

Union (or) - This is expressed with the + symbol. For example (1 + 0) matches either 0 or 1. The expression (00) + (11) matches 00 or 11, while the expression 0(0+1) matches either 00 or 01.

Star - The star operator matches any number (including zero) of repetitions of the starred item. For example 10* matches 1, 10, 100, 1000, etc. The expression (10)* matches 10, 1010, 101010, etc. It also matches the empty string.

Parentheses are used to group operators.

• Consider the regular expression 0*1(0+1)*.
  11. Does this expression match the string 00101100? Does it match the string 0000?
  12. Provide an English language description of the set of strings that this expression matches.
  13. Design a Finite State Machine that recognizes the same set of strings as this regular expression. "Test" your design by checking it with several strings that meet the criteria in different ways.
• Write regular expressions that match the following sets:
  14. The set of all strings that start with a 1 and end with a 1.
  15. The set of strings that are accepted by the FSM associated with questions 1 - 4.
  16. The set of strings that are accepted by the FSM associated with questions 5 - 8.