One-bit Binary Addition
| 0 | 0 | 1 | 1 | |
| + 0 | + 1 | + 0 | + 1 | |
| 00 | 01 | 01 | 10 | |
| carry, sum | 0, 0 | 0, 1 | 0, 1 | 1, 0 |
| input | output | ||
|---|---|---|---|
| A | B | carry | sum |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
What do these results look like?
One-bit Addition
| input | output | ||
|---|---|---|---|
| A | B | carry | sum |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
sum = A XOR B
carry = A AND B
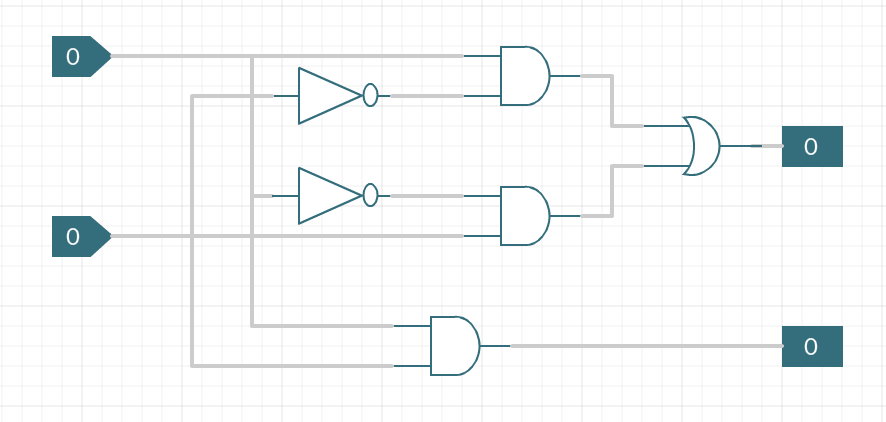
We can also draw this using the other XOR circuit diagram or an XOR gate.NOTE: This does not allow for a carry-in! What about if we want to add numbers that have more than one bit?
This does only half of the total task, and is known as a half-adder.
Binary Addition with carry-in
The way humans do it...
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| + 0 | + 1 | + 0 | + 1 | + 0 | + 1 | + 0 | + 1 | |
| 00 | 01 | 01 | 10 | 00 | 01 | 01 | 10 | |
| carry-in | + 0 | + 0 | + 0 | + 0 | + 1 | + 1 | + 1 | + 1 |
| 00 | 01 | 01 | 10 | 01 | 10 | 10 | 11 | |
| carry, sum | 0, 0 | 0, 1 | 0, 1 | 1, 0 | 0, 1 | 1, 0 | 1, 0 | 1, 1 |
The way computers do it with half-adders
| First HA | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|
| + 0 | + 1 | + 0 | + 1 | + 0 | + 1 | + 0 | + 1 | |
| carry, sum | 0, 0 | 0, 1 | 0, 1 | 1, 0 | 0, 0 | 0, 1 | 0, 1 | 1, 0 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | |
| Second HA | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| carry-in | + 0 | + 0 | + 0 | + 0 | + 1 | + 1 | + 1 | + 1 |
| carry, sum | 0, 0 | 0, 1 | 0, 1 | 0, 0 | 0, 1 | 1, 0 | 1, 0 | 0, 1 |
| Full carry, sum | 1, 0 | 1, 0 | 1, 0 | 1, 1 |
Sum bit: sum bit from the second HA
Carry bit: true if either HA generated a carry
Summary: One-bit Addition With Carry-in
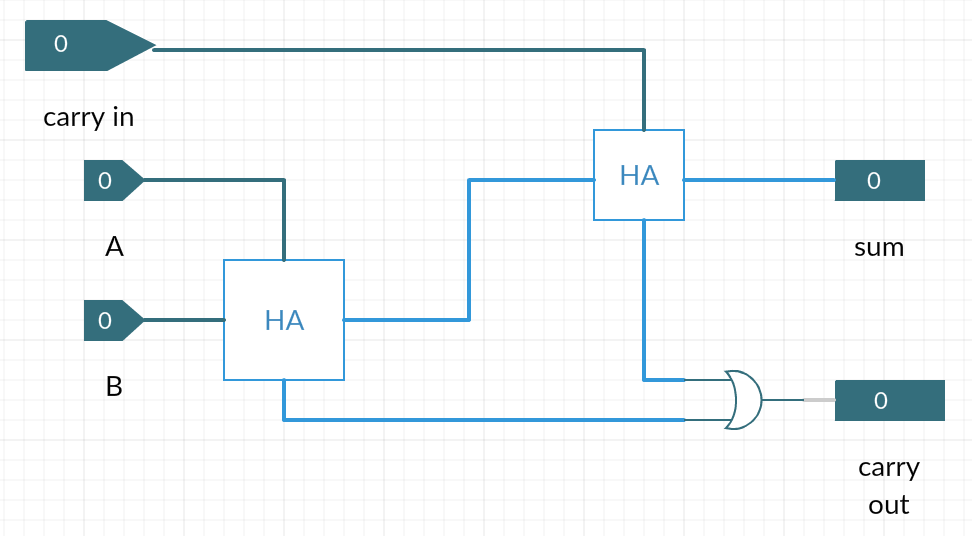
We have two half-adders. The first adds A + B. The sum bit of that is then added to the carryin in the second half-adder. The overall sum is the sum bit from the second add.
sumfull = carryin XOR sumh1
The addition yields a carry if either of the two half-adders yield a carry.
carryout = carryh1 OR carryh2
Next: How do we set up a multi-bit adder?